问题
问答题
设
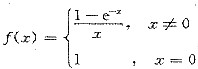 ,求证:
,求证:
(Ⅰ) f(x)在(-∞,+∞)二阶连续可导;
(Ⅱ) f(x)在(-∞,+∞)单调下降;
(Ⅲ) f(x)在(-∞,+∞)是凹的.
答案
参考答案:[分析与证明]
[*]
f(x)在x=0连续.
当x≠0时
[*]
又
[*]
[*],f'(x)在x=0连续.
当x≠0时
[*]
右端是初等函数,在定义域x≠0上连续,即f"(x)在x≠0上连续.又
[*]
[*] f"(0)=[*],f"(x)在x=0也连续.
因此,f"(x)在(-∞,+∞)连续.
(Ⅱ) 令g(x)=ex-(1+x)
[*]
[*] f(x)在(-∞,+∞)单调下降.
(Ⅲ) 考察f"(x)的表达式,令
[*]
[*] h'(x)=ex-(1+x)>0 (x≠0).(题(Ⅱ) 中已证).
[*] h(x)在(-∞,+∞)单调上升,
[*]
因此,f(x)在(-∞,+∞)为凹的.
解析:[*]
