问题
问答题
过坐标原点作曲线
 的切线,该切线与曲线
的切线,该切线与曲线
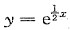 及y轴围成平面图形D.
及y轴围成平面图形D.
(Ⅰ) 求D的面积A;
(Ⅱ) 求D绕y轴旋转一圈所得旋转体体积V.
答案
参考答案:[分析与求解] 为用定积分计算面积和体积,须先求出切线方程,另外,画出草图对分析问题是很有帮助的.设切线的切点坐标为(x0,y0),则切线的斜率为[*],所以切线方程为:[*]x0),注意到[*]于是有[*],因切线过(0,0)点,把x=0,y=0代入上述方程,得x0=2,y0=e,因此所求切线方程为[*].
[*]
(Ⅰ) D的面积是两个曲边梯形面积之差,于是
[*]
(Ⅱ) [解法1] 设[*],y=e,y轴所围平面图形绕y轴旋转一周所得旋转体体积为V1,[*],y=e,y轴所围平面图形绕y轴旋转所得旋转体体积为V2,则V=V1-V2.
V1是圆锥体体积,[*],
对于V2,取积分变量为y,曲线[*]表为x=2lny,则y∈[1,e].dV2=πx2dy=π(2lny)2dy=4πln2ydy,
[*]
[解法2] 取积分变量为x,则x∈[0,2]
[*]
[*]
解析:[*]
