问题
问答题
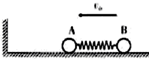
如图所示,质量为4kg的小球A与质量为2kg的小球B,用轻弹簧相连(未栓接)在光滑的水平面上以速度v.向左运动,在A球与左侧墙壁碰撞,碰后两球继续运动的过程中,弹簧的最大弹性势能为8J,假设A球与墙壁碰撞过程中无机械能的损失,求:
①弹簧弹性势能在何时达到最大;
②v0的大小.
答案
①由题意分析可知,A球与左墙壁前后无机械能损失,所以A球与左侧墙壁碰撞后的速度大小仍为v0,
在A球继续运动的过程中,当A,B小球的速度相等时,弹簧的弹性势能最大.
②由于A球与左墙壁碰撞前后无机能损失,所以A球与左侧墙壁碰撞后的速度大小仍为v0,方向水平向右,
对于A、B小球和弹簧组成的系统,在A球与左侧墙壁碰撞到两球速度相等的过程中,规定向右为正方向,
由动量守恒定律有:mAv0-mBv0=(mA+mB)v
解得:v=
v01 3
由机械能守恒定律有:
(mA+mB)v02=1 2
(mA+mB)v2+Ep 1 2
解得:v0=
=(mA+mB) 2mAmB
m/s3
答:①当A,B小球的速度相等时,弹簧的弹性势能最大;
②v0的大小是
m/s.3
