问题
问答题
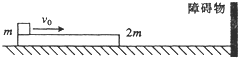
如图所示,在光滑水平地面上有一质量为2m的长木板,其左端放有一质量为m的重物(可视为质点),重物与长木板之间的动摩擦因数为μ.开始时,长木板和重物都静止,现在给重物以初速度v0,设长木板撞到前方固定的障碍物前,长木板和重物的速度已经相等.已知长木板与障碍物发生弹性碰撞,为使重物始终不从长木板上掉下来,求长木板的长度L至少为多少?(重力加速度度为g)
答案
碰撞前,长木板和重物的共同速度为v1,由动量守恒定律得:
mv0=3mv1;
碰撞后瞬间,长木板以速度v1反弹,最终两者的共同速度为v2.由动量守恒定律得:
2mv1-mv1=3mv2;
对全过程,由功能关系得:
μmgL=
m1 2
-v 20
•3m1 2 v 22
联立解得:L=13 v 20 27μg
答:为使重物始终不从长木板上掉下来,长木板的长度至少为
.13 v 20 27μg
