问题
问答题
一厂商有两个工厂,各自的成本由下列两式给出:
工厂1:C1(Q1)=10
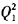
工厂2:C2(Q2)=20
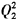
厂商面临如下需求曲线:P=700-5Q,式中Q为总产量,即Q=Q1+Q2。
(1)计算利润最大化的Q1、Q2、Q和P。
(2)假设工厂1的劳动成本增加而工厂2没有提高,厂商该如何调整工厂1和工厂2的产量如何调整总产量和价格
答案
参考答案:一厂商有两个工厂,各自的成本由下列两式给出:
工厂1:C1(Q1)=10[*];
工厂2:C2(Q2)=20[*];
厂商面临如下需求曲线:P=700-5Q,式中Q为总产量,即Q=Q1+Q2。
(1)计算利润最大化的Q1、Q2、Q和P。
(2)假设工厂1的劳动成本增加而工厂2没有提高,厂商该如何调整工厂1和工厂2的产量如何调整总产量和价格
解析:一个能在两个空间上分开的工厂生产产品,其利润是两个工厂总收益与总成本之差:
[*]
分别对Q1和Q2求偏导并令其等于零,得
[*]=700-10Q1-10Q2-20Q1
=700-30Q1-10Q2=0 ……………①
[*]=700-10Q2-10Q1-40Q2
=700-10Q1-50Q2=0…………………………………②
将①式减②式化简得Q1=2Q2,并代入①或②得Q1=20,Q2=10,所以Q=Q1+Q2=30,代入P=700-5Q,得P=550。
(2)假设工厂1劳动成本增加而工厂2没有提高,该厂商会减少工厂1的产量,增加工厂2的产量,并且会使总产量减少,价格提高。
