问题
填空题
过直线x+y-2
|
答案
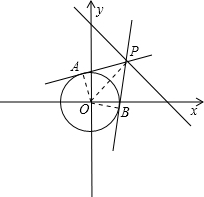
根据题意画出相应的图形,如图所示:
直线PA和PB为过点P的两条切线,且∠APB=60°,
设P的坐标为(a,b),连接OP,OA,OB,
∴OA⊥AP,OB⊥BP,PO平分∠APB,
∴∠OAP=∠OBP=90°,∠APO=∠BPO=30°,
又圆x2+y2=1,即圆心坐标为(0,0),半径r=1,
∴OA=OB=1,
∴OP=2AO=2BO=2,∴
=2,即a2+b2=4①,a2+b2
又P在直线x+y-2
=0上,∴a+b-22
=0,即a+b=22
②,2
联立①②解得:a=b=
,2
则P的坐标为(
,2
).2
故答案为:(
,2
)2
