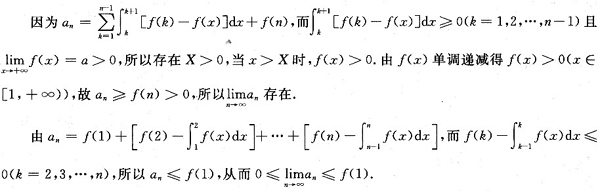问题
问答题
设f(x)在[1，+∞]内可导，f’(x)＜0且
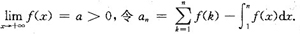证明：an收敛且
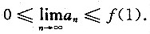
答案
参考答案：因为f’(x)＜0，所以f(x)单调减少．又因为
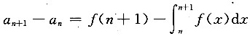
=f(n+1)-f(ξ)≤0(ξ∈[n，n+1])所以{an}单调减少．
搜题请搜索小程序“爱下问搜题”
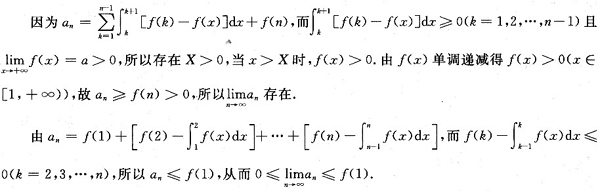
设f(x)在[1，+∞]内可导，f’(x)＜0且
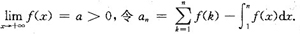证明：an收敛且
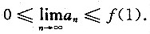
参考答案：因为f’(x)＜0，所以f(x)单调减少．又因为
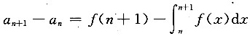
=f(n+1)-f(ξ)≤0(ξ∈[n，n+1])所以{an}单调减少．