问题
问答题
如图所示,光滑水平路面上,有一质量为m1=5kg的无动力小车以匀速率v0=2m/s向前行驶,小车由轻绳与另一质量为m2=25kg的车厢连结,车厢右端有一质量为m3=20kg的物体(可视为质点),物体与车厢的动摩擦因数为μ=0.2,开始物体静止在车厢上,绳子是松驰的.求:

(1)当小车、车厢、物体以共同速度运动时,物体相对车厢的位移(设物体不会从车厢上滑下);
(2)从绳拉紧到小车、车厢、物体具有共同速度所需时间.(取g=10m/s2)
答案
(1)0.017m;(2)0.1s
(1)以m1和m2为研究对象,考虑绳拉紧这一过程,设绳拉紧后,m1、m2的共同速度为v1这一过程可以认为动量守恒,由动量守恒定律有m1v0=(m1+m2)v1,
解得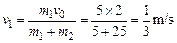 .
.
再以m1、m2、m3为对象,设它们最后的共同速度为v2,则m1v0=(m1+m2+m3)v2,
解得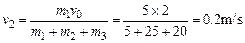
绳刚拉紧时m1和m2的速度为v1,最后m1、m2、m3的共同速度为v2,设m3相对m2的位移为Δs,则在过程中由能量守恒定律有
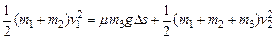
解得Δs=0.017m.
(2)对m3,由动量定理,有μm3gt=m3v2
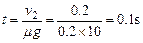
所以,从绳拉紧到m1、m2、m3有共同速度所需时间为t=0.1s.
