(一)
已知某家庭2010年12月31日购买价值50万元的住房一套,申请了相当于房价70%的住房抵押贷款,期限20年、年利率6%、按月等额还本付息。同时,该家庭拟于5年后,也就是2016年1月1日,购买第二套住房。为此,该家庭除了还第一套住宅的贷款外,还将工资收入的50%储蓄用于购买第二套住房,该家庭月工资收入为12000元,预计将以每月0.5%的比例递增,该家庭购买第二套住房时拟以第一套住房申请二次住房抵押贷款(又称“加按”,假设按产权人拥有的权益价值的50%发放),而不再申请第二套住房抵押贷款。已知当地住宅价值年上涨率为5%,银行存款年利率为3%,按月计息。问该家庭能承受的第二套住房的最高总价是多少
参考答案:
(1)2016年1月1日第一套住房的市场价值
V=500000×(1+5%)5=638140.8元
(2)第一抵押贷款月还款额
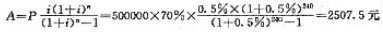
(3)2016年1月1日未偿还的第一套住房的第一抵押贷款价值
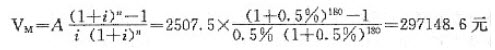
(4)该家庭拥有的住房权益价值
VE=V-WM=638140.8-297148.6=340992.2元
(5)第二次抵押可获得的最大抵押贷款额为
P1=340992.2×50%=170496.10元
(6)工资收入中可用于购房款的现值
P2=A1/(i-s){1-[(1+s)/(1+i)]n}
=12000×50%/(0.25%-0.5%)×{1-[(1+0.5%)/(1+0.25%)]60}
=386840.23元
(7)工资收入中可用于购房款的终值:P3=P2×(1+0.25%)60=449360.10元
(8)该家庭能承受的第二套住房的最高总价
P=P1+P3=170496.10+449360.10=619856.2元。
