问题
单项选择题
用积分法计算下图所示梁的挠曲线微分方程时间,其正确的边界条件和连续条件应为()。
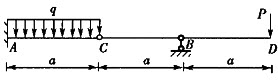
A.边界条件 当x=0时,yA=0,y’A=0;当x=2a时,yB=0
连续条件 当x=a时,yC左=yC右,y’C左=y’C右;当x=2a时,yB左=yB右,y’B左=y’B右
B.边界条件 当x=0时,yA=0,y’A=0;当x=2a时,yB=0
连续条件 当x=a时,yC左=yC右;当x=2a时,yB左=yB右,y’B左=y’B右
C.边界条件 当x=0时,yA=0;当x=2a时,yB=0
连续条件 当x=a时,yC左=yC右;当x=2a时,yB左=yB右
D.边界条件 当x=0时,yA=0,y’A=0;当x=2a时,yB=0
连续条件 当x=a时,yC左=yC右,y’C左=y’C右;当x=2a时,yB左=yB右,y’B左=y’B右
答案
参考答案:B
解析:
注意在固定端挠度和转角均为零,在铰支座处挠度为零,在铰联接处只有两侧的挠度相等,而在刚性连接处两侧的挠度和转角均要相等,因此正确答案为(B)。