问题
问答题
设矩阵
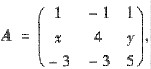
已知A有3个线性无关的特征向量,λ=2是A的二重特征值.
(1)确定参数x,y;
(2)求可逆矩阵P,使P-1AP为对角矩阵.
答案
参考答案:(1)A有3个线性无关的特征向量,λ=2是二重特征值,故A属于λ=2的线性无关特征向量有2个,即方程组(2E-A)X=0的系数矩阵满足3-r(2E-A)=2,亦即
r(2E-A)=1.
[*]
于是[*]即[*]
(2)由于λ1+λ2+λ3=1+4+5,从而λ3=6.
当λ1=λ2=2时,
[*]
特征向量为η1=(1,-1,0)T,η2=(1,0,1)T
当λ=6时
[*]
[*]
特征向量为η3=(1,-2,3)T
令[*],则
[*]
解析:[考点] 使带有参数的矩阵相似对角化
