问题
填空题
- A．条件(1)充分，但条件(2)不充分
- B．条件(2)充分，但条件(1)不充分
- C．条件(1)和条件(2)单独都不充分，但条件(1)和条件(2)联合起来充分
- D．条件(1)充分，条件(2)也充分
- E．条件(1)和条件(2)单独都不充分，条件(1)和条件(2)联合起来也不充分
数列{an}的奇数项与偶数项按原顺序分别组成公比不等于1的等比数列．
(1) 数列{an}中，
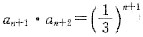，其中n∈N
(2) 数列{an
答案
参考答案：A
解析： 由条件(1)，显然各项均不会为零，又[*]，则有
[*]
an与an+2之间间隔一项，这说明数列{an}中奇数项依次组成的数列或者偶数项依次组成的数列均为以[*]为公比的等比数列，所以条件(1)充分．
由条件(2)，{an}是等比数列，因而它的奇数项或偶数项所组成的数列仍然是等比数列，但应注意一个特殊情况，就是原数列有可能是一个非零常数数列，此时数列本身以及它的奇数项或偶数项所组成的数列均为公比等于1的等比数列，所以条件(2)不充分．
故选A．