问题
问答题
设连续函数f(x)满足方程
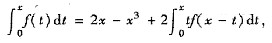 求f(x).
求f(x).
答案
参考答案:[解] 令u=x-t作换元,则t:0→x[*]u:x→0,且t=x-u,dt=-du,代入即得
[*]
从而原方程可改写为
[*]
因f(x)连续,2x-x3可导,故上式中各项都可导.将上式两端对x求导数,就有
[*](*)
在(*)式中令x=0可得f(0)=2,又因(*)式右端各项都可导,从而f(x)可导.将(*)式两端对x求导可得
f’(x)=-6x+2f(x).
综上可知f(x)是如下一阶线性微分方程初值问题的特解
[*]
用积分因子e-2x同乘方程两端得 (e-2xy)’=-6xe-2x.积分得
[*]
于是方程的通解是[*].利用初值y(0)=2可确定常数[*].故所求的函数
[*]
