问题
问答题
设f(x)在[1,3]上连续,在(1,3)内可导,试证:存在两点ξ,η∈(1,3),使得
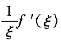 =
=
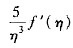 .
.
答案
参考答案:[证明] 取g(x)=x2,则由题设知f(x)与g(x)都在[1,3]上连续,在(1,3)内可导,且g’(x)=2x≠0在x∈(1,3)成立,从而由柯西定理知:存在ξ∈(1,3)使得
[*]
取h(x)=x4,则由题设知f(x)与h(x)都在[1,3]上连续,在(1,3)内可导,且h’(x)=4x3≠0在x∈(1,3)成立,从而由柯西定理知:存在η∈(1,3)使得
[*]
由此可得
[*]
