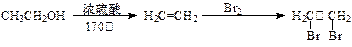问题
填空题
设矩阵A=
 ,矩阵B满足ABA*=2BA*+E,其中A*为A的伴随矩阵,E是单位矩阵,则|B|=______.
,矩阵B满足ABA*=2BA*+E,其中A*为A的伴随矩阵,E是单位矩阵,则|B|=______.
答案
参考答案:[*]
解析:[考点提示] 矩阵运算、行列式.
[解题分析] 由题设,A=[*],则|A|=3≠0,从而由公式AA*=A*A=|A|E,知A*=|A|A-1=3A-1,则|A*|=33·3-1=9.将ABA*=2BA*+E变形为(A-2E)BA*=E,则|A-2E||B||A*|=|E|,其中
[*]
所以|B|=[*]

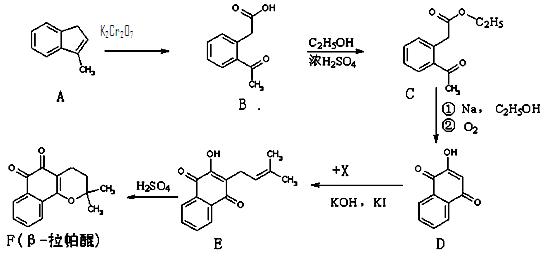
 、“E→F”)。
、“E→F”)。 : ▲ 。
: ▲ 。 子中有一个醛基和一个羧基
子中有一个醛基和一个羧基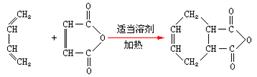 ,
,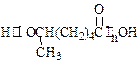 。
。