问题
问答题
设当x>0时,方程kx+
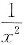 =1有且仅有一个解,求k的取值范围.
=1有且仅有一个解,求k的取值范围.
答案
参考答案:设f(x)=[*],则f(x)在(0,+∞)内连续,且
[*]
令f’(x)=0,解得f(x)在(0,+∞)内的唯一驻点x=[*],且为极大值点,极大值为
[*]
又
[*]
且y=f(x)的图像在(0,[*])区间内凹.可见,当k=[*]以及k≤0时,曲线y=f(x)与直线y=k且仅有一个交点,即方程kx+[*]=1有且仅有一个解.
解析:[考点提示] 一般说来,方程f(x)=g(x)有解x0,等价于相应的曲线y=f(x)与y=g(x)在点(x0,y0)处相交,其中y0=f(x0)=g(x0).注意到当x>0时,方程[*]同解.可设f(x)=[*],g(x)=k,于是方程kx+[*]=1在(0,+∞)内有且仅有一个解,亦即曲线y=f(x)与直线y=k在右半平面(x>0)内有且仅有一个交点.若曲线y=f(x)的值域一旦确定,则k的取值范围自然也十分明确了.
[评注] 也可令f(x)=kx+[*]-1,并讨论在k取何值时函数在x>0时只有一个零点.
