问题
问答题
设二维随机变量(X,Y)的联合概率密度函数为
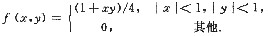
证明:X与Y不独立,但X2与Y2独立.
答案
参考答案:[详解] 首先有
[*]
因为f(x,y)≠fX(x)fY(y),所以x,y不独立.
[*]
U=X2,V=Y2的联合分布函数为
[*]
可见,对U=X2,V=Y2而言,有F(u,υ)=FU(u)FV(υ),
即X2和Y2相互独立.
解析:
[分析]: 两个随机变量X,Y独立[*]F(x,y)=FX(x)FY(y)或f(x,y)=FX(x)FY(y).因此判断两个随机变量是否独立可从分布函数或概率密度函数进行分析.
[评注] 对于离散型随机变量,一般不用分布函数或概率密度检验,而用联合分布律与边缘分布律:X与Y相互独立[*]P(X=xi,Y=yi)=P(X=xj)·P(Y=yj).
