设二维随机变量(X,Y)服从区域G上的均匀分布,G是由x-y=0,x+y=2与y=0围成的三角形区域.
①求X的概率密度fX(x);②求条件概率密度fX|Y(x|y).
参考答案:易知SG=1
则
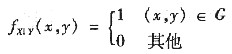
x<0或x>2时fX(x)=0
当0<x≤1时,
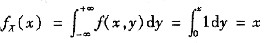
当1<x<2时,
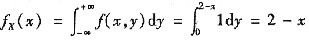
综上
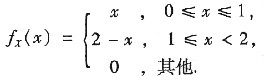
当y≥1或y<0时fY(y)=0
当0≤y<1时
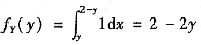
则
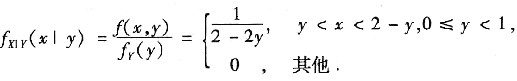
解析:[考点] 条件概率密度、联合密度
设二维随机变量(X,Y)服从区域G上的均匀分布,G是由x-y=0,x+y=2与y=0围成的三角形区域.
①求X的概率密度fX(x);②求条件概率密度fX|Y(x|y).
参考答案:易知SG=1
则
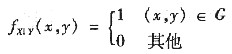
x<0或x>2时fX(x)=0
当0<x≤1时,
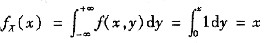
当1<x<2时,
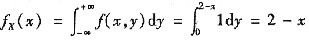
综上
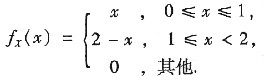
当y≥1或y<0时fY(y)=0
当0≤y<1时
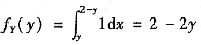
则
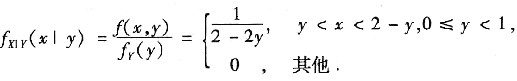
解析:[考点] 条件概率密度、联合密度