问题
问答题
设A为三阶实对称矩阵，r(A)=2，且
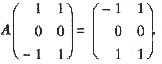
(Ⅰ) 求A的所有特征值与特征向量；
(Ⅱ) 求A．
答案
参考答案：(Ⅰ)
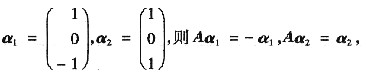根据特征值特征向量的定义，A的特征值为λ1=-1，λ2=1，对应的线性无关的特征向量为
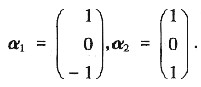
因为r(A)=2＜3，所以|A|=0，故λ3=0．
令
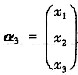为矩阵A的相应于λ3=0的特征向量，因为A为实对称矩阵，所以有
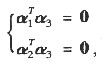即
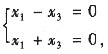解得
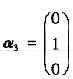．故矩阵A的特征值为1，-1，0；特征向量依次为k1(1，0，1)T，k2(1，0，-1)T，k3(0，1，0)T．其中k1，k2，k3是不为0的任意常数．
(Ⅱ) α1，α2，α3单位化得
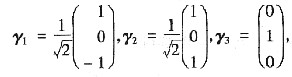
令
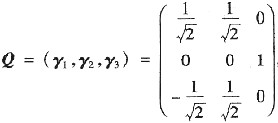，则
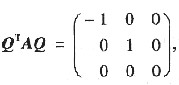
于是
解析：[考点] 矩阵的特征值和特征向量