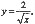问题
问答题
求通过点（1，2）的曲线方程，使此曲线在[1，x]上形成的曲边梯形面积的值等于此曲线弧终点的横坐标x与纵坐标y乘积的2倍减去4．
答案
参考答案：
依题意，有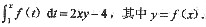
两端对x求导，得 y=2y+2xy’，
从而 2xy’=-y， 即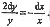
解此微分方程，得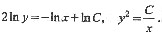
将y(1)=2代入，得出C=4． 所求曲线方程为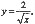
搜题请搜索小程序“爱下问搜题”
求通过点（1，2）的曲线方程，使此曲线在[1，x]上形成的曲边梯形面积的值等于此曲线弧终点的横坐标x与纵坐标y乘积的2倍减去4．
参考答案：
依题意，有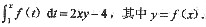
两端对x求导，得 y=2y+2xy’，
从而 2xy’=-y， 即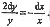
解此微分方程，得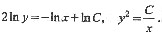
将y(1)=2代入，得出C=4． 所求曲线方程为