参考答案：

证：因为f是满射的，所以对于任意的b∈B，g(b)≠Φ。若g非单射，必存在b₁，b₂∈B，且b≠b，使得g(b₁)=g(b₂)。于是，对任意的x，x∈g(b₁)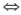x∈g(b₂)，而

x∈g(b₁)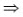f(x)=b₁（1）

x∈g(b₂)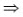f(x)=b₂（2）

由（1）（2）可知b₁=b₂，这与b₁≠b₂矛盾。所以g是单射的。