问题
问答题
设G是一个顶点个数为n（n≥5）、边数为m的连通平面图，如果G的最小圈的长度为5，证明：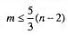
。
答案
参考答案：
证：设G的面的个数为f。因为G的最小圈的长度为5，故G的每个面的度数（也称为‘次数’）至少为5.由于面的度数之和等于边数的两倍，故5f≤2m，即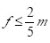
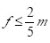。将代入欧拉公式n-m+f=2，解得
。
搜题请搜索小程序“爱下问搜题”
设G是一个顶点个数为n（n≥5）、边数为m的连通平面图，如果G的最小圈的长度为5，证明：。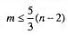
参考答案：
证：设G的面的个数为f。因为G的最小圈的长度为5，故G的每个面的度数（也称为‘次数’）至少为5.由于面的度数之和等于边数的两倍，故5f≤2m，即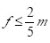。将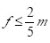代入欧拉公式n-m+f=2，解得。