问题
问答题
设函数
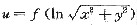 ,满足
,满足
 ,且极限
,且极限
 ,试求函数f的表达式.
,试求函数f的表达式.
答案
参考答案:[详解] 设[*]
[*]
积分两次得[*],即[*]
又[*],从而有f(0)=0,f’(0)=-2,将其代入
f(x)表达式中,得[*]
故所求函数f的表达式为[*]
解析:
[分析]: 先求出二阶导数,代入已知关系式后,可得一微分方程,再按标准方法进行求解即可.注意,本题的初始条件是通过极限[*]确定的,此条件相当于告诉了f(x)在点x=0处的函数值与导数值.
[评注] 通过导数定义或偏导数引出微分方程是值得注意的一种题型,而初始条件由传统的直接告之f(0)=0,f’(0)=-2,转化为通过极限[*]给出,这种可能的命题形式更应引起重视.
