本电视机生产厂家去年销往农村的某品牌电视机每台的售价y(元)与月份x之间满足函数关系y=-50x+2600,去年的月销售量p(万台)与月份x之间成一次函数关系,其中每个月的销售情况如下表:
| 月份 | 1月 | 5月 |
| 销售量 | 3.9万台 | 4.3万台 |
(1)求该品牌电视机在去年哪个月销往农村的销量金额最大最大是多少
(2)由于受国际金融危机的影响,今年1、2月份该品牌电视机销往农村的售价都比去年12月份下降了m%,且每月的销售量都比去年12月份下降了1.5m%.国家实施“家电下乡”政策,即对农村家庭购买新的家电产品,国家按该产品售价的13%给予了财政补贴.受此政策的影响,今年3至5月份,该厂家销售到农村的这种电视机在保持今年2月份的售价不变的情况下,平均每月的销售量比今年2月份增加了1.5万台.若今年3至5月份国家对这种电视机的销售共给予了财政补贴936万元,求m的值(保留一位小数).
参考答案:
(1)设p与x的函数关系为P=kx+b(k≠0),根据题意,得:
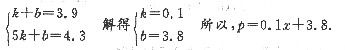
设月销售金额为ω万元,则
ω=py=(0.1x+31.8)(-50x+2600),
化简,得ω=-5x2+70x+9880,
所以,ω=-5(x-7)2+10125.
当x=7时,叫取得最大值,最大值为10125.
答:该品牌电视机在去年7月份销往农村的销售金额最大,最大是10125万元.
(2)去年12月份每台的售价为-50×12+2600=2000(元),
去年12月份的销售量为0.1×12+3.8=5(万台),
根据题意,得2000(1-m%)×[5(1-1.5m%)+1.5]×13%×3=936。
令m%=t,原方程可化为7.5t2-14t+5.3=0.
∴t1≈0.528,t2≈1.339(舍去).
答:m的值约为52.8.
