问题
问答题
设总体X服从[0，θ]上的均匀分布，θ未知(θ＞0)，X1，X2，X3是取自X的一个样本．
(1)试证：
，
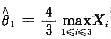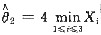都是θ的无偏估计；
(2)上述两个估计中哪个方差较小
答案
参考答案：[详解] (1)设F(x)是X的分布函数，则 [*]
令[*]，则
FY(x)=[F(x)]3，[*]
FZ(x)=1-[1-F(x)]3，[*]
于是 [*]
故[*]均为θ的无偏估计量．
[*]
可见[*]的方差比[*]的方差小．
解析：
[分析]： 为了求出[*]，[*]的期望与方差，应先确定它们的分布，而极值分布可用已有公式求出，再根据期望与方差的定义计算即可．
[评注] 设X1，X2，…，Xn相互独立同分布，分布函数为F(x)，
则max{X1，X2，…，Xn}的分布函数为Fmax(x)=Fn(x)．
而min{X1，X2，…，Xn)的分布函数为Fmin(x)=1-[1-F(x)]n．