问题
问答题
设曲面∑是锥面
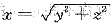 与两球面x2+y2+z2=1,x2+y2+z2=2所围立体表面的外侧,计算曲面积分
与两球面x2+y2+z2=1,x2+y2+z2=2所围立体表面的外侧,计算曲面积分
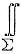 x3dydz+(y3+f(yz))dzdx+(z3+f(yz))dxdy
x3dydz+(y3+f(yz))dzdx+(z3+f(yz))dxdy
其中f(u)是连续可微的奇函数.
答案
参考答案:[详解] 记∑所围区域为Ω,则
[*]
由题设f(u)为奇函数,于是f’(u)为偶函数,
根据Ω关于z=0对称,zf’(yz)关于z为奇函数,从而有[*]
Ω关于y=0对称,yf’(yz)关于y为奇函数,从而有[*]
故 [*]
解析:
[分析]: ∑为封闭曲面且取外侧,自然想到用高斯公式,转化为三重积分进行计算.空间立体为球体的一部分,可采用球面坐标计算,在计算过程中,还应注意利用对称性进行简化.
[评注] 本题Ω关于平面x=0是非对称的,因此当被积函数关于x为奇函数时,也不能得到关于相应三重积分为零的结论.
