问题
问答题
设四元齐次线性方程组(Ⅰ)为
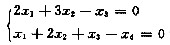
而另一四元齐次线性方程组(Ⅱ)的一个基础解系为
α1=(2,-1,a+2,1)T,α2=(-1,2,4,a+8)T
(1)求方程组(Ⅰ)的一个基础解系;
(2)当a为何值时,方程组(Ⅰ)与(Ⅱ)有非零公共解在有非零公共解时,求出全部非零公共解.
答案
参考答案:(1)对方程组(Ⅰ)的系数矩阵作初等行变换,有
[*]
得方程组(Ⅰ)的基础解系为
β1=(5,-3,1,0)T,β2=(-3,2,0,1)T。
(2)设γ是方程组(Ⅰ)和(Ⅱ)的非零公共解,则
γ=x1β1+x2β2=-x3α1-x4α2
那么 x1β1+x2β2+x3α1+x4α4=0.
对系数矩阵A=(β1,β2,α1,α2)作初等行变换,有
[*]
当a=-1时
[*]
得基础解系
η1=(-1,-1,1,0)T,η2=(-4,-7,0,1)T
所以Ax=0的通解为
k1η1+k2η2=(-k1-4k2,-k1-7k2,k1,k2)T
故方程组(Ⅰ)和(Ⅱ)的公共解
[*]
