问题
问答题
用变量代换x=cost(0<t<π)化简微分方程(1-x2)y"-xy’+y=0,并求其满足
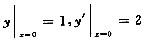 的特解.
的特解.
答案
参考答案:建立y对t的一、二阶导数与y对x的一、二阶导数之间的关系:
[*]
从而原方程可化为y=y(t)满足的微分方程[*]不难得出这个方程的通解是y=C1cost+C2sint.将cost=x与当0<t<π时[*]即得原方程的通解为[*]
由初值[*]
故所求特解为[*]
解析:[评注] 本题是一个二阶线性变系数方程,按题目中指出的变量代换可把它化为新变量的函数满足二阶常系数线性微分方程的初值问题,从而可求解.
