问题
问答题
设函数z=f(xy,yg(x)),其中函数f具有二阶连续偏导数,函数g(x)可导且在x=1处取得极值
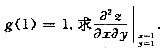
答案
参考答案:[*]
因为g(x)可导且在x=1取极值,从而g’(1)=0,又g(1)=1,于是
[*]
故
[*]
=f’(1,1)+f"11(1,1)+f"12(1,1).
[评注] 求得
[*]
后,可先求出任意点处的[*]得
[*]
=[xf"11+g(x)f"12]y+f’1+[xf"21+g(x)f"22]yg’(x)+g’(x)f’2.再令x=1,y=1,并由g(1)=1,g’(1)=0,xy=1,yg(x)=1最后仍可得
[*]
但这比前面的解法要复杂些.
[*]
往往会简化计算.
偏导数实质上是一元函数的导数.
