问题
问答题
求连续函数f’(x),使它满足
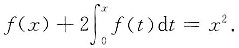
答案
参考答案:方程[*]两边对x求导得
f’(x)+2f(x)=2x,
令x=0,由原方程得f(0)=0.
于是,原问题就转化为求微分方程f’(x)+2f(x)=2x满足初始条件f(0)=0的特解.
由一阶线性微分方程的通解公式,得
[*]
代入初始条件f(0)=0,得[*]
从而[*]
解析:[考点提示] 先在等式两边对x求导,消去变限积分,将原方程化为关于未知函数f(x)的微分方程,再求解该微分方程.
[评注1] 对于含有变限积分的函数方程问题,一般先在等式两边对x求导,消去变限积分,将原方程化为关于未知函数的微分方程,再求解该微分方程.
[评注2] 本题虽然只给出f(x)是连续函数,实际上,隐含着f(x)可导.因为变限积分[*]可导,所以[*]可导.
[评注3] 由含有变限积分的函数方程转化为微分方程,一般隐含着初始条件,应在原方程中确定初始条件.
