问题
问答题
设m元线性方程组Ax=b,其中
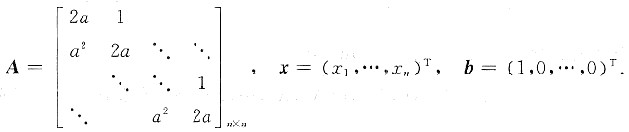
(Ⅰ) 证明行列式|A|=(n+1)an;
(Ⅱ) a为何值时,方程组有唯一解求x1;
(Ⅲ) a为何值时,方程组有无穷多解求通解.
答案
参考答案:(Ⅰ) 利用行列式性质,有
[*]
[*]
(Ⅱ) 若方程组Ax=b有唯一解,则|A|=(n+1)an≠0,即a≠0.则由克莱姆法则得
[*]
(Ⅲ) 若使方程组Ax=b有无穷多解,则|A|=(n+1)an=0,即a=0.
把a=0代入到矩阵A中,显然有[*],方程组的基础解系含一个解向量.它的基础解系为k(1,0,0,…,0)T(k为任意常数).代入a=0后方程组化为[*]特解取为(0,1,0,…,0)T,则方程组Ax=b的通解为
k(1,0,0,…,0)T+(0,1,0,…,0)T,其中的k为任意常数.
解析:[考点提示] 线性方程组解的结构和通解.
