问题
问答题
设函数f(x)处处可导，
试证：
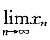存在，且满足方程x=f(x)．
答案
参考答案：先证{xn}单调．
由xn+1-xn=f(xn)-f(xn-1)=(xn-xn-1)f’(ξn)，其中ξn在xn与xn-1之间．
又由题设，f(x)处处可导，且[*]，于是知f’(ξn)≥0，从而(xn+1-xn)与(xn-xn-1)同号，故{xn}单凋．
再证{xn}有界．
[*]
综上所述知，{xn}单调有界．故由极限存在准则知，[*]存在．
设[*]，因f(x)处处可导，故f(x)处处连续，而xn=f(xn-1)，于是有
[*]
则 A=f(A)，即满足方程x=f(x)．
解析：
[分析]： 利用极限存在准则证明．