问题
填空题
已知抛物线y2=2px(p＞0)，过定点(p，0)作两条互相垂直的直线l1、l2，l1与抛物线交于P、Q两点，l2与抛物线交于M、N两点，l1斜率为k．某同学已正确求得弦PQ的中点坐标为
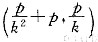，请写出弦MN的中点坐标：（）．
答案
参考答案：(pk2+p，-pk)
解析：
[专家点评] 由l1与抛物线交于两点可知，k≠0，由于l1、l2互相垂直，故l2的斜率为[*]．
设M(x1，y1)、N(x2、y2)，则[*]
两式相减得，(y1-y2)(y1+y2)=2p(x1-x2)，
∴[*]，则y1+y2=2pk，
∴弦MN中点纵坐标为-pk，又因为l2过定点(p，0)，所以由[*]可得x=pk2+p，故中点坐标为(pk2+p，-pk)．