问题
问答题
设α1，α2，α3线性无关，β1=(m-1)α1+3α2+α3，β2=α1+(m+1)α2+α3，β3=α1-(m+1)α1+(1-m)α2，其中m为实数，讨论m与r(β1，β2，β3)的关系．
答案
参考答案：
本题思路：βi与αi构成了矩阵相乘的关系，AB=C，讨论这个矩阵的关系．
(β1，β2，β3)=((m-1)α1+3α2+α3，α1+(m+1)α2+α3，α1-(m+1)α2+(1-m)α3)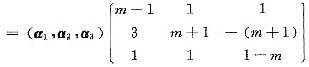
由于β1，β2，β3线性无关，r(α1，α2，α3)=3=(α1，α2，α3)的列数．根据性质，如果r(A)等于列数，则r(AB)=r(B)，由此可得
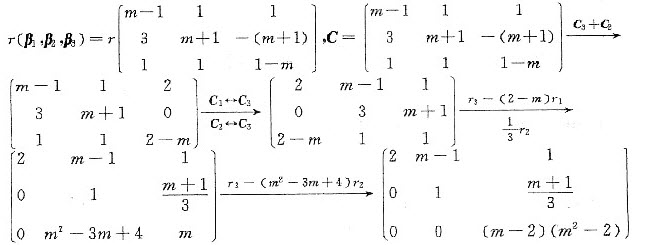(1)若(m-2)(m2-2)=0，即m=2或m=±
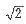，r(C)=2，r(β1，β2，β3)=r(C)=2．
(2)若(m-2)(m2-2)≠0，即m≠2且m≠±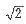，r(C)=3，r(β1，β2，β3)=r(C)=3．