问题
问答题
设含n个方程的齐次线性方程组
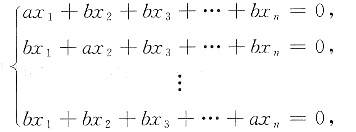
其中a≠0,b≠0,n≥2.试讨论a、b为何值时,方程组仅有零解、无穷多组解在有无穷多解时,求出全部解,并用基础解系表示全部解。
答案
参考答案:由题设,方程组的系数矩阵为
[*]
则
[*]
当a≠b且a+(n-1)b≠0,即a≠(1-n)b时,方程组仅有零解.
当a=b时,对A可作初等行变换化为阶梯形
[*]
则不难求得原方程组的基础解系为
[*]
因此方程组的全部解是x=k1ξ1+k2ξ2+…+kn-1ξn-1,其中k1,k2,…,kn-1为任意常数.
当a=(1-n)b时,同样对A作初等行变换化为阶梯形
[*]
则可得此时基础解系为[*],从而原方程组的全部解是妊,其中k为任意常数.
解析:[考点提示] 线性齐次方程组.
