问题
问答题
设二次型f(x1,x2,x3)=
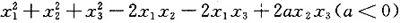 通过正交变换化为标准形
通过正交变换化为标准形
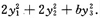
1.求常数a,b;
答案
参考答案:令
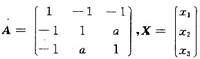 则f(x1,x2,x3)=XTAX.
则f(x1,x2,x3)=XTAX.
因为二次型经过正交变换化为
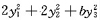 所以矩阵A的特征值为λ1=λ2=2,λ3=b.由特征值的性质得
所以矩阵A的特征值为λ1=λ2=2,λ3=b.由特征值的性质得
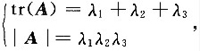 即
即
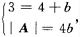 解得a=-1,b=-1
解得a=-1,b=-1
设二次型f(x1,x2,x3)=
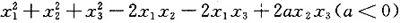 通过正交变换化为标准形
通过正交变换化为标准形
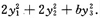
1.求常数a,b;
参考答案:令
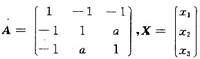 则f(x1,x2,x3)=XTAX.
则f(x1,x2,x3)=XTAX.
因为二次型经过正交变换化为
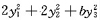 所以矩阵A的特征值为λ1=λ2=2,λ3=b.由特征值的性质得
所以矩阵A的特征值为λ1=λ2=2,λ3=b.由特征值的性质得
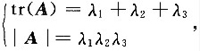 即
即
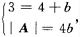 解得a=-1,b=-1
解得a=-1,b=-1