问题
问答题
设f(x)在[0,1]上连续,(0,1)内二阶可导,且
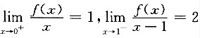 证明:
证明:
1.存在ζ∈(0,1),使得f(ζ)=0;
答案
参考答案:令φ(x)=exf(x),由f(0)=f(ζ)=f(1)=0,得φ(0)=φ(ζ)=φ(1)=0.由罗尔定理,存在ζ1∈(0,ζ),ζ2∈(ζ,1),使得φ’(ζ1)=ζ’(ζ2)=0.又φ’(x)=ex[f(x)+f’(x)],则f(ζ1)+f(ζ1)=0,f(ζ2)+f’(ζ2)=0.
令g(x)=e-x[f(x)+f’(x)],则g(ζ1)=g(ζ2)=0,再由罗尔定理,存在η∈(ξ1,ξ2),使得g’(η)=0,而g’(x)=e-x[f"(x)~f(x)],所以f"(η)-f(η)=0,即f"(η)=f(η).
