问题
问答题
设二次型
经正交变换x=Py化成
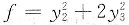，其中x=(x1，x2，x3)T和y=(y1，y2，y3)T是三维列向量，P是3阶正交矩阵．试求常数α，β．
答案
参考答案：变换前后二次型的矩阵分别为
[*]
二次型可以写成f=xTAx和f=yTBy．
由于PTAP=B，P为正交矩阵，故PTAP=B．
因此|λE-A|=|λE-B|，
即
[*]
λ3-3λ2+(2-α2-β2)λ+(α-β)2=λ3-3λ2+2λ，
比较系数得α=β=0．
解析：[评注] 这是二次型标准化中的逆问题，即已知二次型的标准形，反求原二次型中的未知参数，这种逆向思维的命题方式应引起重视．
[考点提示] 经正交变换(注意不是非退化线性变换)化二次型为标准形，前后二次型所对应的矩阵必相似，从而有相同的特征多项式，由此可确定参数α、β．