问题
问答题
设总体X~U[0,θ],其中θ>0,求目的极大似然估计量,判断其是否是θ的元偏估计量.
答案
参考答案:总体X的密度函数和分布函数分别为

设x1,x2,…,xn为总体X的样本观察值,似然函数为
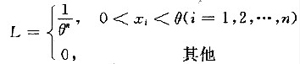
当0<x1<θ(i=1,2,…,n)时,
 且当θ越小时L(θ)越大,所以θ的最大似然估计值为
且当θ越小时L(θ)越大,所以θ的最大似然估计值为
 ,θ的最大似然估计量为
,θ的最大似然估计量为
 。
。
因为
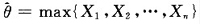 的分布函数为
的分布函数为


设总体X~U[0,θ],其中θ>0,求目的极大似然估计量,判断其是否是θ的元偏估计量.
参考答案:总体X的密度函数和分布函数分别为

设x1,x2,…,xn为总体X的样本观察值,似然函数为
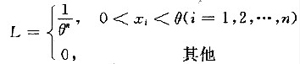
当0<x1<θ(i=1,2,…,n)时,
 且当θ越小时L(θ)越大,所以θ的最大似然估计值为
且当θ越小时L(θ)越大,所以θ的最大似然估计值为
 ,θ的最大似然估计量为
,θ的最大似然估计量为
 。
。
因为
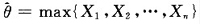 的分布函数为
的分布函数为

