问题
问答题
一电子仪器由两个部件构成,以X和Y分别表示两个部件的寿命(单位:千小时),已知X和Y的联合分布函数为
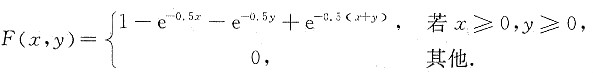
(1) 问X和Y是否独立
(2) 求两个部件的寿命都超过100小时的概率α.
答案
参考答案:[详解1] 由题设条件知X和Y的分布函数分别为
[*]
(1) 由上式知F(x,y)=FX(x)FY(y),故X和Y相互独立.
(2) α=P{X>0.1.Y>0.1}=P{X>0.1}P{Y>0.1}
=(1-P{X≤0.1})(1-P{y≤0.1})
=[1-FX(0.1)][1-FY(0.1)]
=e-0.1.
[详解2] 以f(x,y)、fX(x)和fY(y)分别表示(X,Y)、X和Y的概率密度,则
[*]
(1) 由f(x,y)=fX(x),(y),知X和Y相互独立.
(2) α=P{X>0.1,Y>0.1}=P{X>0.1}P{Y>0.1}
[*]
解析:[评注1] 本题主要考查二维随机变量独立性的判定和概率的计算.
对任意二维随机变量(X,Y),有X、Y相互独立[*]F(x,y)=FX(x)FY(y);
对二维连续型随机变量(X,Y)有X和Y相互独立[*]f(x,y)=fX(x)fY(y);
对二维离散型随机变量(X,Y)有X和Y相互独立
[*]P{X=xi,Y=yi}=P{X=xi)P{Y=yi}.
[评注2] 若X、Y不独立,则第(2)问可用下列公式求解
P{X>a,Y>b
