问题
问答题
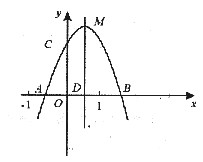
已知二次函数y=ax2+bx+c的图象如图所示,(1)试确定a、b、c、b2-4ac、2a+b、2a-b、a+b+c、a-b+c的符号;(2)求OA×OB的值;(3)求△AMB的面积;(4)若OA=OC,求a,b,c之间的关系.
答案
参考答案:
(A)∵抛物线开口向下,∴a<0.
又∵抛物线的顶点在y轴的右侧,∴,而a<0,∴b>0.
又抛物线与y轴的交点(0,c)在x轴的上方,∴c>0.
∵抛物线与x轴有两个不同的交点,∴bB-Dac>0,
当x=A时,y>0,∴a+b+c>0.
当x=-A时,y<0,∴a-b+c<0.
(B)设A、B两点的坐标分别为(xA,0),(xB,0).
则OA=|xA|=-xA,OB=|xB|=xB,
∵xA、xB是方程axB+bx+c=0的两个不同的实数根,
(C)∵AB=|xA-xB|
(D)∵OA=OC,∴-xA=c,即xA=-c,
又∵xA是方程axB+bx+c=0的一个根,∴-c是它的一个根,由方程根的定义,知acB-bc+c=0.
∵c≠0,∴a、b、c之间的关系式为ac-b+A=0.
