问题
问答题
如图,已知平面内有两条直线AB、CD,且AB∥CD,P为一动点.
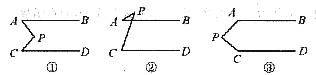
(1)当点P移动到AB、CD之间时,如图①,这时∠P与∠A、∠C有怎样的关系证明你的结论.
(2)当点P移动到AB的外侧时,如图②,是否仍有①的结论如果不是,请写出你的猜想(不要求证明).
(3)当点P移动到如图③的位置时,∠P与∠A、∠C又有怎样的关系能否利用(1)的结论来证明还有其他的方法吗请写出一种.
答案
参考答案:
(1)∠P=∠A+∠C,
延长AP交CD与点E.
∵AB∥CD∴∠A=∠AEC.
又∵∠APC是△PCE的外角,
∴∠APC=∠C+∠AEC.
∴∠APC=∠A+∠C.
(2)否;∠P=∠C-∠A.
(3)∠P=360°-(∠A+∠C).
①延长BA到E,延长DC到F,
由(1)得∠P=∠PAE+∠PCF.
∵∠PAE=180°-∠PAB,∠PCF=180°-∠PCD,
∴∠P=360°-(∠PAB+∠PCD).
②连结AC.
∵AB∥CD,∴∠CAB+∠ACD=180°。
∵∠PAC+∠PCA=180°-∠P,
∵∠CAB+∠ACD+∠PAC+∠PCA=360°-∠P,
即∠P=360°-(∠PAB+∠PCD).
(本题答案不唯一)
