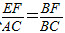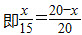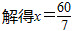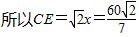问题
填空题
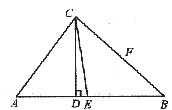
如图,在△ABC中,CD是高,CE为∠ACB的平分线,若AC=15,BC=20,CD=12,则CE的长等于().
答案
参考答案:
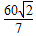
解析:
如图,由勾股定理知AD=9,BD=16,所以AB=AD+BD=25.
故由勾股定理逆定理知△_ACB为直角三角形,且∠ACB=90°.
作EF⊥BC,垂足为F,设EF=x,由[*]45°,得CF=x,于是BF=20-x,由于EF∥AC,
所以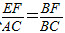
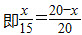
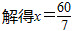
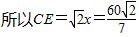
如图,在△ABC中,CD是高,CE为∠ACB的平分线,若AC=15,BC=20,CD=12,则CE的长等于().

参考答案:
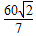
解析:
如图,由勾股定理知AD=9,BD=16,所以AB=AD+BD=25.
故由勾股定理逆定理知△_ACB为直角三角形,且∠ACB=90°.
作EF⊥BC,垂足为F,设EF=x,由[*]45°,得CF=x,于是BF=20-x,由于EF∥AC,
所以