问题
问答题
设函数
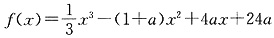，其中常数a＞1．
(1)讨论f(x)的单调性；
(2)若当x≥0时，f(x)＞0恒成立，求a的取值范围.
答案
参考答案：
(1)f′(x)=x2-2(1+a)x+4a=(x-2)(x-2a)，
由a＞1知，当x＜2时，f′(x)＞0，故f(x)在区间(-∞，2)是增函数；
当2＜x＜2a时，f′(x)＜0，故f(x)在区间(2，2a)是减函数；
当x＞2a时，f′(x)＞0，故f(x)在区间(2a，+∞)是增函数，
综上，当a＞1时，f(x)在区间(-∞，2)和(2a，+∞)是增函数，在区间(2，2a)是减函数．
(2)由(1)知，当x≥0时，f(x)在x=2a或x=0处取得最小值，
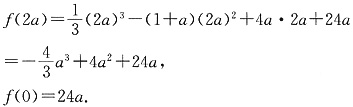
由假设知
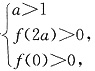即
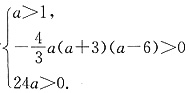，解得1＜a＜6．
故a的取值范围是(1，6).