问题
问答题
(Ⅰ)叙述二元函数z=f(x,y)在点(x0,y0)处可微及微分
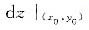 的定义;
的定义;
(Ⅱ)证明下述可微的必要条件定理:设z=f(x,y)在点(x0,y0)处可微,则f’x(x0,y0)与f’y(x0,y0)都存在,且
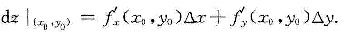
(Ⅲ)举例说明(Ⅱ)的定理之逆不成立.
答案
参考答案:定义:设z=f(x,y)在点(x0,y0)的某邻域U内有定义,(x0+△x,y0+△y)∈U.增量
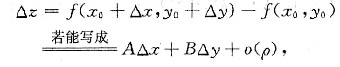
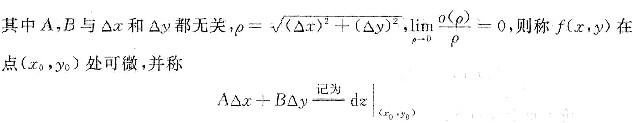
为z=f(x,y)在点(x0,y0)处的微分.
(Ⅱ)设z=f(x,y)在点(x0,y0)处可微,则(Ⅰ)式成立.命△y=0,于是
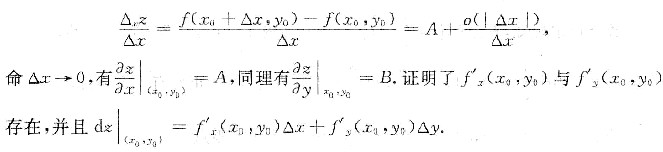
(Ⅲ)当f’x(x0,y0)与f’y(x0,y0)存在时z=f(x,y)在点(x0,y0)处未必可微.反例:设
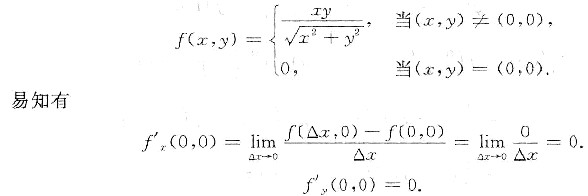
两个偏导数存在,以下用反证法证出f(x,y)在点(0,0)处不可微.若可微,则有
△f=f(△x,△y)-f(0,0)=0△x+0△y+o(ρ),