设矩阵
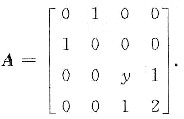
(1) 已知A的一个特征值为3,试求y;
(2)求矩阵P,使(AP)T(AP)为对角矩阵.
参考答案:(1) 因为
[*]
当λ=3时,代入上式解得y=2.于是
[*]
(2) 方法一 由AT=A,得(AP)T(AP)=PTA2P,
而矩阵[*]
考虑二次型
[*]
令y1=x1,y2=x2.[*],y4=x4,得
[*]
取[*]
则有[*]
方法二 先求出A2的特征值λ1=1(三重),λ2=9.
对应于λ1=1的特征向量为
α1=(1,0,0,0)T,α2=(0,1,0,0)T,α3=(0,0,-1,1)T.
经正交并单位化后,得向量组β1=(1,0,0,0)T,β2=(0,1,0,0)T
对应于λ2=9的特征向量为α4=(0,0,1,1,)T,经单位化后,得
[*]
令[*]
则[*]
解析:[考点提示] 由定义有|3E-A|=0,由此可定出参数y.考虑到A2为对称矩阵,而(AP)T(AP)=PTA2P,化其对角矩阵方法有两种:转化为对应二次型xTA2x,通过非退化线性变换x=Py化为标准形,相应求出P;或者求出A2的特征值、单位化,最后构造出正交矩阵P,本题所求P不唯一.
[评注] 将一个实对称矩阵化为对角阵可用二次型的配方法也可用正交变换法,但两者是有本质区别的.用配方法得到的对角阵的对角线上的元素不一定是矩阵特征值,得到的可逆矩阵P也不一定是正交的,而正交变换法得到的对角线上的元素一定是矩阵特值,得到可逆矩阵P也一定是正交的.
