问题
问答题
如图，在三菱锥S-ABC中，平面SAB⊥平面SBC，AB⊥BC，AS=AB，过A作AF⊥SB，垂足为F，点E，G分别是棱SA，SC的中点。求证：
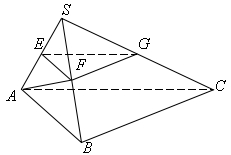
BC⊥SA
答案
参考答案：
因为平面SAB⊥平面SBC，平面SAB∩平面SBC=BC，
AF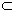
平面ASB，AF⊥SB。
所以，AF⊥平面SBC。
又BC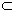平面SBC。
所以，AF⊥BC。
又AB⊥BC，AF∩AB=A，
所以，BC⊥平面SAB。
又SA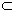平面SAB，
所以，BC⊥SA。