问题
解答题
已知函数f(x)=2
（I ）求f（x）的最小正周期； （Ⅱ）若将f（x）的图象按向量
|
答案
（I）f(x)=
sin(x+3
)+sinπ 2
…（2分）x
=2(
sinx+1 2
cosx)=2sin(x+3 2
)…（4分）π 3
所以f（x）的最小正周期为2π…（5分）
（Ⅱ）∵将f（x）将f（x）的图象按向量
=(a
，0)平移，得到函数g（x）的图象．π 6
∴g(x)=f(x-
)=2sin[(x-π 6
)+π 6
]=2sin(x+π 3
)…（9分）π 6
∵x∈[0，π]，x+
∈[π 6
，π 6
]7π 6
∴函数g（x）的增区间为[0，
]，减区间为[π 3
，π]π 3
∵sin(x+
)∈[-π 6
，1]1 2
∴2sin(x+
)∈[-1，2]π 6
∴函数g（x）值域[-1，2]…（10分）
缺失，余牙正常，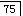
作为基牙所选用的卡环是（）