问题
单项选择题
下列关于反常积分
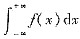 的四个命题:
的四个命题:
①设f(x)是(-∞,+∞)上连续的奇函数,则
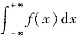 必收敛,且
必收敛,且
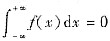
②设f(x)是(-∞,+∞)上连续,且
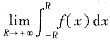 存在,则
存在,则
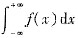 必收敛,且
必收敛,且
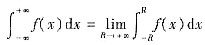
③若
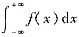 与
与
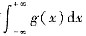 都发散,则
都发散,则
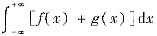 未必发散
未必发散
④若
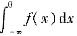 与
与
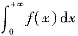 都发散,则
都发散,则
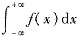 未必发散
未必发散
正确的命题个数为( ).
答案
参考答案:A
解析:众所周知的是,讨论一个反常积分时,要求其区间上的奇点(瑕点和无穷大)个数有且仅有一个,这是一个基本问题,于是,对于反常积分[*],其收敛的充分必要条件是存在常数a,使两个反常积分[*]和[*]都收敛,定义
[*]
设f(x)=x,则f(x)是(-∞,+∞)上连续的奇函数,且[*].但是[*]=[*],[*],故[*]发散,这表明命题①,②,④都不正确.
设f(x)=xg(x)=-x,由上面讨论可知[*]与[*]都发散,但[*]+g(x)]dx收敛,这表明命题③是正确的.故答案选择(A).
