问题
问答题
已知函数f(x)=(x2-3x+3)·ex定义域为[-2，t](t＞-2)，设f(-2)=m，f(t)=n．
求证：对于任意的t＞-2，总存在x0∈（-2，t），满足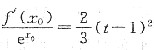
，并确定这样的x0的个数．
答案
参考答案：
[证明] 因为[*]，所以[*]即为[*]，
令[*]，从而问题转化为证明方程[*]在(-2，t)上有解，并讨论解的个数．
因为[*](t-1)，所以①当t＞4或-2＜t＜1时，g(-2)·g(t)＜0，所以g(x)=0在(-2，t)上有解，且只有一解．
②当1＜t＜4时，g(-2)＞0，g(t)＞0，但由于[*]，所以g(x)=0在(-2，t)上有解，且有两解．
③当t=1时，g(x)=x2-x=0[*]x=0或x=1，所以g(x)=0在(-2，t)上有且只有一解；
当t=4时，g(x)=x2-x=0[*]x=-2或x=3，所以g(x)=0在(-2，4)上也有且只有一解．
综上所述，对于任意的t＞-2，总存在x0∈(-2，t)，满足[*]，
且当t≥4或-2＜t≤1时，有唯一的x0适合题意；当1＜t＜4时，有两个x0适合题意．
(说明：第(3)题也可以令φ(x)=x2-x，x∈(-2，t)，然后分情况证明[*]在其值域内，并讨论直线[*]与函数φ(x)的图像的交点个数即可得到相应的x0的个数)